Variance Shadow Maps(分散シャドウマップ)を実装した
Variance Shadow Maps(分散シャドウマップ)を実装しようと思う。
これはソフトシャドウの実装の一つで、シャドウのエッジをなんかいい感じにする技術だ。
まず、普通のシャドウマップの実装を再掲する。
bool IsVisibleFromDirectionalLight(float4 shadowCoord) {
float w = 1.0f / shadowCoord.w;
float2 stex = float2((1.0f + shadowCoord.x * w) * 0.5f, (1.0f - shadowCoord.y * w) * 0.5f);
float depth = DirectionalShadowMap.Sample(ShadowSampler, stex.xy).x;
if (shadowCoord.z * w <= depth + 0.00005f) {
return true;
}
return false;
}
まず、ライト視点のカメラを仮定してパースペクティブ・ビュー行列を作成し、シーンの深度を保存する。
そして、実際のレンダリングパスで対象の頂点を再度ライト視点に復元、格納済みの深度と比較してシャドウ判定を行う。
格納された深度よりも描画対象の深度が低ければシャドウなし、高ければシャドウありだ。
しかし、この2値的なアルゴリズムだと、どうしてもエッジが硬い違和感のあるシャドウになってしまう。これは、シャドウマップの解像度が低くなればよりジャギーが発生し違和感が顕著になる。
リアルの世界のシャドウと言えば、硬いエッジものはそうは見かけない。なぜなら、光源が面積を持っていたり、あるいはシャドウに間接光が入射するなど、様々な影響が存在するからだ。しかし、残念ながら現在はそのどちらも実装できていないので、シャドウのエッジを”誤魔化す”ことにする。
そこで登場するのがVariance Syadow Mapsだ。この手法は、物理的には正しくないが、それなりに見栄えの良いソフトシャドウを作ることができる。更に、これの優れた点は、現状多く存在するシャドウの実装と容易に組み合わせることが可能な点だ。
以下に示すのは、Variance Shadow Maps(以下VSM)の実装に使われる、確率論分野のチェビシェフの不等式である。
ここでtが確率論でいう標本、μが平均値、σが分散である。
これをシャドウマップに適用するのが、Variance Shadow Mapsだ。確率論の不等式をシャドウマップに適用というと突拍子もない話だが、この式によって得られる「0~1に正規化された確率」を「影の濃さとして適用する」と言えばなんとなく想像はつくだろうか。
ここで、チェビシェフの不等式に使う平均値(期待値)、分散だが、これは局所平均値を用いることで計算できる。
その計算方法とは、すなわちシャドウマップにぼかしフィルタを適用した後の値だ。例えば、移動平均フィルタのカーネルは一様分布であるので、そのフィルタを適用した後の各テクセルの値は局所平均値になることは自明であろう。(元論文)http://www.punkuser.net/vsm/vsm_paper.pdfでは、ガウシアンフィルタを使うようだ。
シャドウマップには現状、深度ステンシルバッファを使っている。残念ながらこれは最も最適な手法だが融通が利かないので、深度バッファではなくレンダーターゲットに焼き付ける手法でシャドウマップを作成する。レンダーターゲットを使えば、1つのピクセルにつきrgbaの4つのスロットを使うことができる。rに深度を、ついでにgに深度の2乗を格納しておくことで、まとめてE(x), E(x^2)を計算することができる。
というわけで、DirectXで実装してみよう。DirectXには、GPU上のリソースに手を加えるという軟弱な機能はないので(CPUにマップすれば可能だが無駄すぎる)、ガウスフィルタを適用したいテクスチャと同じサイズのビューポートを作り、そこに画面いっぱいに板ポリゴンを配置、ガウスフィルタを適用しながらその板ポリゴンを描画すると、レンダーターゲットにガウスフィルタの適用したテクスチャのできあがりだ。
レンダーターゲットに深度を焼きこむピクセルシェーダは省略でいいだろう。zとz^2を出力するだけだ。
ガウスフィルタは、X-PassとY-Passに分離できるので、2つのシェーダーを作り2パスに分けて描画することにする。
X-Pass
struct pixcelIn
{
float4 pos : SV_POSITION;
float2 tex : TEXCOORD;
};
Texture2D txDiffuse : register(t0);
SamplerState samLinear : register(s0);
cbuffer ConstantBuffer : register(b0)
{
float4 weight1;
float4 weight2;
float2 texsize;
}
float4 main(pixcelIn In) : SV_Target
{
float MAP_WIDTH = texsize.x;
float3 col = weight1.x * txDiffuse.Sample(samLinear, float2(In.tex) + float2(+1.0f / MAP_WIDTH, 0));
col += weight1.y * (txDiffuse.Sample(samLinear, In.tex + float2(+3.0f / MAP_WIDTH, 0)) + txDiffuse.Sample(samLinear, In.tex + float2(-3.0f / MAP_WIDTH, 0)));
col += weight1.z * (txDiffuse.Sample(samLinear, In.tex + float2(+5.0f / MAP_WIDTH, 0)) + txDiffuse.Sample(samLinear, In.tex + float2(-5.0f / MAP_WIDTH, 0)));
col += weight1.w * (txDiffuse.Sample(samLinear, In.tex + float2(+7.0f / MAP_WIDTH, 0)) + txDiffuse.Sample(samLinear, In.tex + float2(-7.0f / MAP_WIDTH, 0)));
col += weight2.x * (txDiffuse.Sample(samLinear, In.tex + float2(+9.0f / MAP_WIDTH, 0)) + txDiffuse.Sample(samLinear, In.tex + float2(-9.0f / MAP_WIDTH, 0)));
col += weight2.y * (txDiffuse.Sample(samLinear, In.tex + float2(+11.0f / MAP_WIDTH, 0)) + txDiffuse.Sample(samLinear, In.tex + float2(-11.0f / MAP_WIDTH, 0)));
col += weight2.z * (txDiffuse.Sample(samLinear, In.tex + float2(+13.0f / MAP_WIDTH, 0)) + txDiffuse.Sample(samLinear, In.tex + float2(-13.0f / MAP_WIDTH, 0)));
col += weight2.w * (txDiffuse.Sample(samLinear, In.tex + float2(+15.0f / MAP_WIDTH, 0)) + txDiffuse.Sample(samLinear, In.tex + float2(-15.0f / MAP_WIDTH, 0)));
return float4(col, 1.0f);
}Y-Pass
struct pixcelIn
{
float4 pos : SV_POSITION;
float2 tex : TEXCOORD;
};
Texture2D txDiffuse : register(t0);
SamplerState samLinear : register(s0);
cbuffer ConstantBuffer : register(b0)
{
float4 weight1;
float4 weight2;
float2 texsize;
}
float4 main(pixcelIn In) : SV_Target
{
float MAP_HEIGHT = texsize.y;
float3 col = weight1.x * txDiffuse.Sample(samLinear, float2(In.tex));
col += weight1.y * (txDiffuse.Sample(samLinear, In.tex + float2(0, +2.0f / MAP_HEIGHT)) + txDiffuse.Sample(samLinear, In.tex + float2(0, -2.0f / MAP_HEIGHT)));
col += weight1.z * (txDiffuse.Sample(samLinear, In.tex + float2(0, +4.0f / MAP_HEIGHT)) + txDiffuse.Sample(samLinear, In.tex + float2(0, -4.0f / MAP_HEIGHT)));
col += weight1.w * (txDiffuse.Sample(samLinear, In.tex + float2(0, +6.0f / MAP_HEIGHT)) + txDiffuse.Sample(samLinear, In.tex + float2(0, -6.0f / MAP_HEIGHT)));
col += weight2.x * (txDiffuse.Sample(samLinear, In.tex + float2(0, +8.0f / MAP_HEIGHT)) + txDiffuse.Sample(samLinear, In.tex + float2(0, -8.0f / MAP_HEIGHT)));
col += weight2.y * (txDiffuse.Sample(samLinear, In.tex + float2(0, +10.0f / MAP_HEIGHT)) + txDiffuse.Sample(samLinear, In.tex + float2(0, -10.0f / MAP_HEIGHT)));
col += weight2.z * (txDiffuse.Sample(samLinear, In.tex + float2(0, +12.0f / MAP_HEIGHT)) + txDiffuse.Sample(samLinear, In.tex + float2(0, -12.0f / MAP_HEIGHT)));
col += weight2.w * (txDiffuse.Sample(samLinear, In.tex + float2(0, +14.0f / MAP_HEIGHT)) + txDiffuse.Sample(samLinear, In.tex + float2(0, -14.0f / MAP_HEIGHT)));
return float4(col, 1.0f);
}フィルタの重みは以下のように計算できる。
struct GaussianCBuffer { float weight[8]; Size texsize; }; AlignedBuffer<GaussianCBuffer> buf; float total = 0; constexpr float disperision = 10.0f; for (int i = 0; i < 8; i++) { float pos = 1.0f + 2.0f * (float)i; buf.weight[i] = std::expf(-0.5f * pos * pos / disperision); if (i == 0) { total += buf.weight[i]; } else { total += 2.0f * buf.weight[i]; } } for (int i = 0; i < 8; i++) { buf.weight[i] /= total; }
ここでdisperisionパラメータは、シャドウの見栄えがよくなる適切なパラメータを指定する。
このシェーダーで描画されたシャドウマップのrとbを使って、"影になる確率"を求める。(実際には確率を濃度として使うのでこの表現には語弊がある)
float GetVarianceDirectionalShadowFactor(float4 shadowCoord) {
float w = 1.0f / shadowCoord.w; // 頂点シェーダでGPUは勝手にwでx, y, zを割る。その再現
float2 stex = float2((1.0f + shadowCoord.x * w) * 0.5f, (1.0f - shadowCoord.y * w) * 0.5f); // -1 ~ 1を 0 ~ 1にマッピング
float2 depth = DirectionalShadowMap.Sample(ShadowSampler, stex.xy).xy;
float depth_sq = depth.x * depth.x; // E(x)^2
float variance = depth.y - depth_sq; // σ^2 = E(x^2) - E(x^2)
variance = min(1.0f, max(0.0f, variance + 0.0001f));
float fragDepth = shadowCoord.z * w;
float md = fragDepth - depth.x; // t - μ
float p = variance / (variance + (md * md)); // σ^2 / (σ^2 + (t - μ)^2)
return max(p, fragDepth <= depth.x); // P(x >= t)を満たすときのみ
}
あとはこれで得られるファクターを、ライティング結果に掛けるだけだ。
VSM実装前と実装後の比較画像を貼る。
VSM
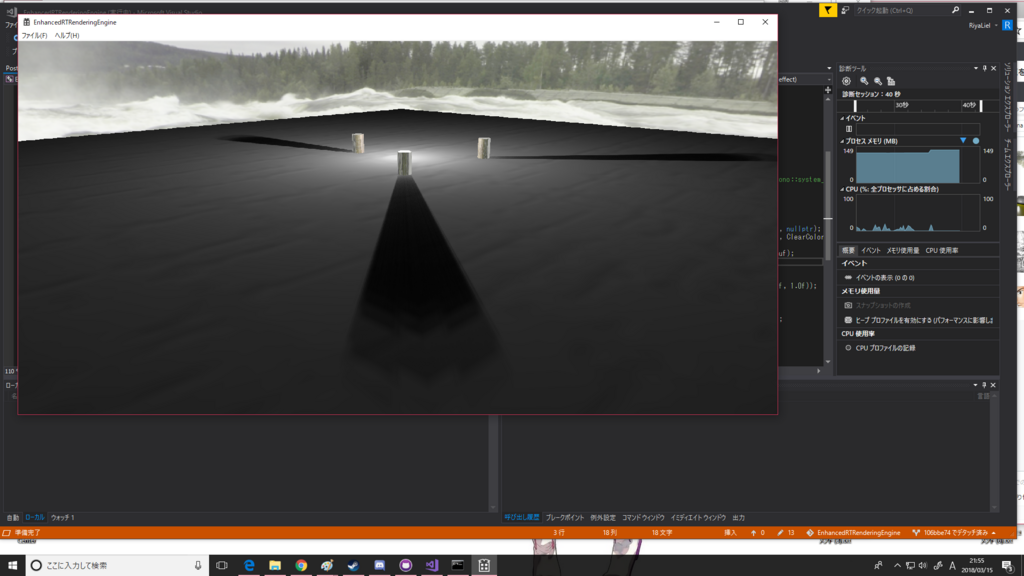
Not VSM
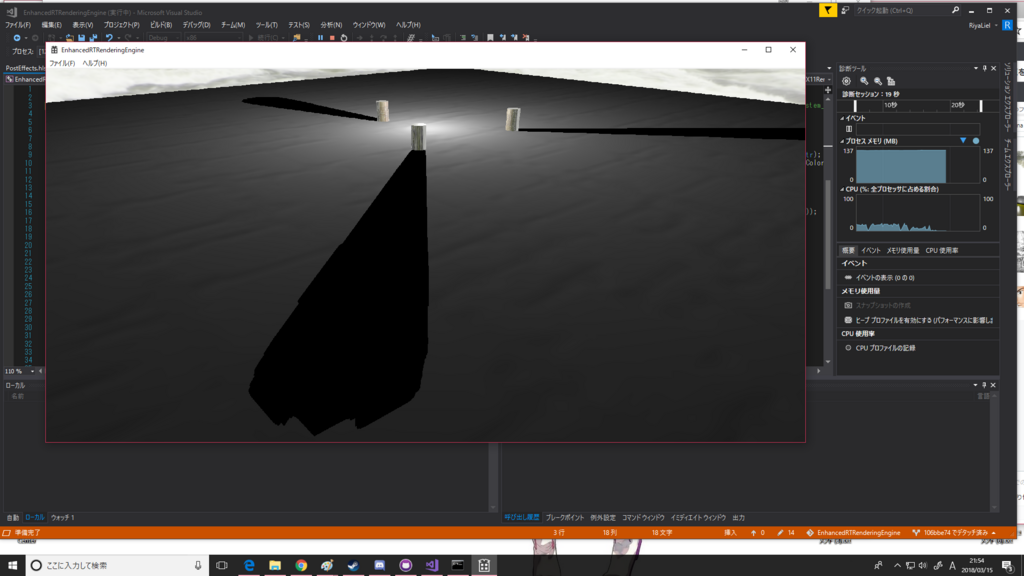
うむ。ソフトになった....うん? うん...(論文とちょっと違う感じになってるのが気になる。ソフトというより残像っぽい)
今回はここまで。